Задачи с практическим содержанием

Впервые задачи с практическим содержанием встречаются в учебнике Л. Ф. Магницкого «Арифметика», который вышел в свет в 1703 году. Задания, содержащиеся в данной книге, имели практическую направленность, например, покупка товаров, раздел имущества, измерение веса и другое.

Приведем пример такой задачи из учебника «Арифметика»: «Купил некто трех сукон 108 аршин; единого взял 12-ю больше перед другим, а другого 9-ю больше перед третьим, и ведательно есть, колико коего сукна взято было» (пояснение к переводу: купил три вещи, х первой, у второй и z третьей, сколько каждой вещи).

Например, предлагается решить такую задачу: «Деревня должна была оградить выгон на протяжении 600 м. Сколько понадобится для этого кольев и жердей, если на каждые 10 м изгороди идет 5 кольев и 8 жердей? Во сколько времени загородят выгон 4 человека, если каждый будет делать в день 50 м изгороди?».

В учебнике «Арифметика 5-6 класс» автора Н. А. Принцева, изданном в 1966 году, представлены задачи, содержание которых связано с производственными вопросами или знакомит школьников с особенностями обработки деталей, созданием изделий, особенностями работы или перемещений каких-либо механизмов.

Железная полоса весом 17,90 кг при обработке потеряла 0,1 своего веса. Сколько она весила после обработки?

В коробке передач автомашины «ЗИЛ-150» зубчатое колесо ведущего вала, имеющее 17 зубцов, сцеплено с другим колесом, имеющим 40 зубцов (рисунок 1). Первое колесо сделало 400 оборотов. Сколько оборотов сделало второе колесо?

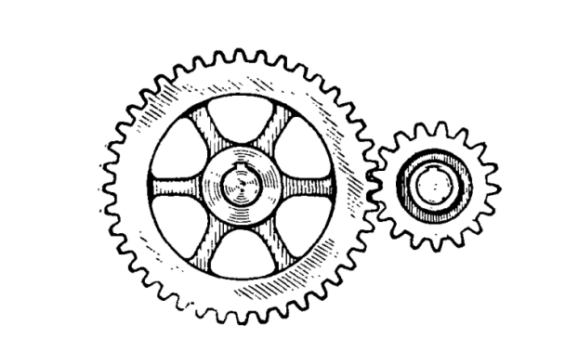
Рисунок 1 – Изображение к задаче на обороты

Если анализировать содержание учебников, включенных в федеральный перечень учебников по алгебре и геометрии с 7 по 11 классы, то можно отметить, что в них содержится достаточно большое количество задач с практическим применением.

А в учебнике «Геометрия. 9 класс» авторов С. А. Козловой, А. Г. Рубина и В. А. Гусева выделен отдельный раздел «Жизненные задачи», что подчеркивает важность рассмотрения задач с практическим содержанием при изучении школьного курса математики и способствует подготовке учащихся к применению полученных знаний в повседневной жизни.

1. Семья Ивановых затеяла ремонт в квартире. Когда дело дошло до установки телевизора, решили встроить его в стену. Специально для этого в стене сделали нишу высотой 90 см и шириной 140 см (рисунок 2). Какую оптимальную диагональ должен иметь телевизор? Учесть, что кроме диагоналей, телевизор имеет рамку корпуса. Ответ укажите в дюймах для рамки корпуса 2 см, 5 см, 7 см.

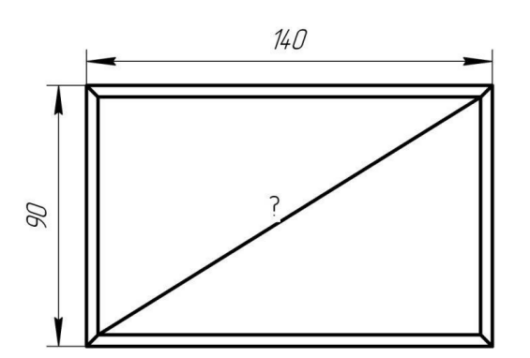
Рисунок 2 – Условие задачи 1

2. Заканчивая ремонт, семья Ивановых столкнулась с проблемой выбора ковра на пол. На рисунке 3 дано расположение объектов в комнате, их размеры и размеры комнаты. Какую площадь пола можно застелить ковром (продумайте варианты расположения ковра и определите его площадь).

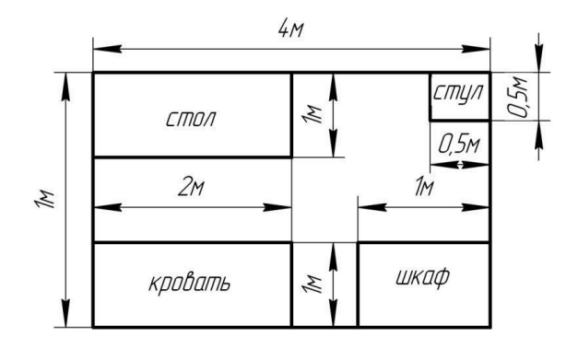
Рисунок 3 – Условие задачи 2

3. Аня и Катя решили встретиться на вокзале. Они условились о том, что каждая из них пройдет свой маршрут до вокзала пешком. Путь девочек 23 указан на рисунке 4. Сколько времени (в минутах) придется ждать той, которая придет быстрее, если средняя скорость движения составляет 5 км/ч?

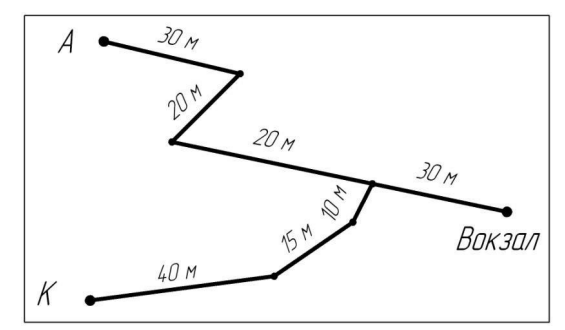
Рисунок 4 – Условие задачи 3

4. Рыбаку нужно измерить ширину водоема до пунктов А и В. Пункты расположены на противоположных берегах водоема (рисунок 5). Рыбак убедился в том, что угол А прямой, и измерил расстояние от пункта А до С, оно составляет 24 м. От пункта В до С – 26 м. Какова протяженность водоема между пунктами А и В?

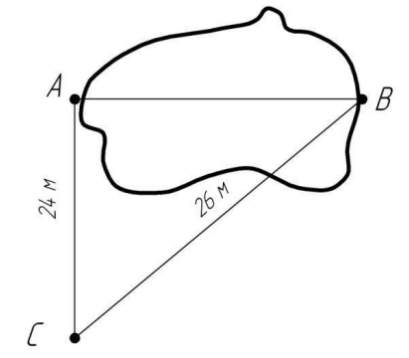
Рисунок 5 – Условие задачи 4

5. Семья выехала из пункта M в пункт N и проехала 50 км. После этого они поехали в пункт K, дорога до которого оказалась в 1,5 раза длиннее, чем из пункта М в пункт N. Дороги MN и NK расположены под прямым углом (рисунок 6). Найдите расстояние между пунктами N и К.

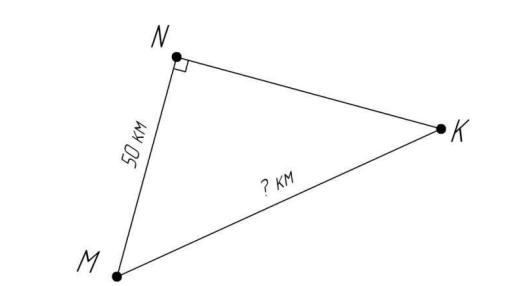
Рисунок 6 – Условие задачи 5

6. Сергею необходимо выполнить ремонтные работы на фасаде дома на высоте 3,5 м от уровня земли (рисунок 7). Для этого он хочет использовать приставную лестницу, но не уверен в том, что ему хватит длины лестницы. В инструкции по использованию приставной лестницы сказано, что безопасный угол установки составляет 30℃. Вычислите длину лестницы и расстояние от стены дома до лестницы. Ответ округлите до сотых.

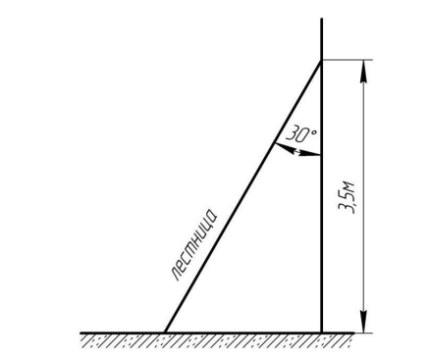
Рисунок 7 – Условие задачи 6

7. Артему нужно купить аквариум нестандартной формы. Эскиз аквариума с размерами показан на рисунке 8. Вычислите объем воды, который
может вместить этот аквариум.

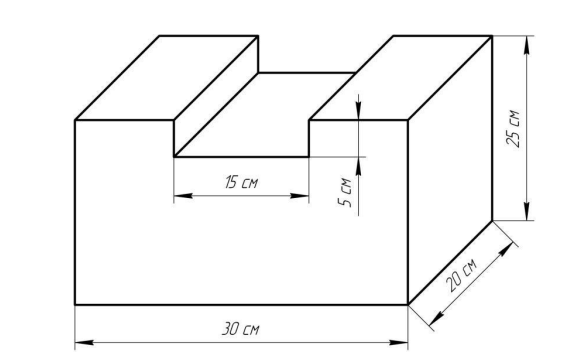
Рисунок 8 – Условие задачи 7

8. Кондитер испек 3 коржа для торта в круглой форме, диаметр которой 20 см. Высота каждого коржа получилась 3 см. На покрытие каждого коржа кремом высотой 1 см потребовалось 300 гр. крема (рисунок 9). Вычислите, сколько граммов крема уйдет на весь торт.

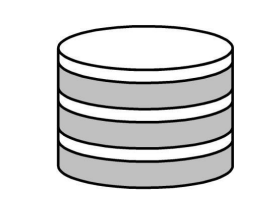
Рисунок 9 – Иллюстрация к задаче 8

9. У начинающего пчеловода имеются три улья (рисунок 10), ширина и длина каждого равна 50 см. Высота самого низкого – 60 см. Оставшиеся два улья в 2 раза выше первого. Известно, что улей объемом 0,30 м3 вмещает в себя 16 рамок, с каждой из которых можно собрать по 3 литра меда. Сколько литров меда пчеловод скачает со всех ульев вместе?

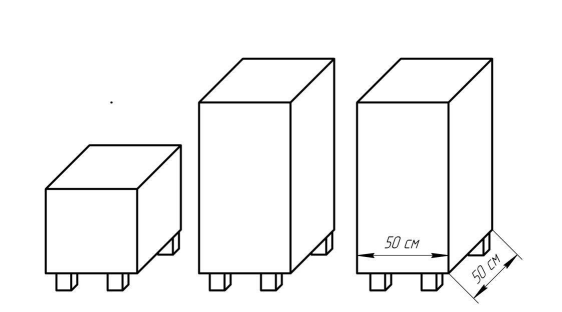
Рисунок 10 – Условие задачи 9

10. Мама для дочки решила сшить юбку солнце. Она начертила выкройку из двух концентрических окружностей. Длина одной из этих окружностей равна обхвату талии девочки – 62,8 см, а радиус второй больше радиуса первой на 60 см (рисунок 11). Вычислите длину окружности по нижнему краю юбки. Сколько метров ткани надо иметь для пошива такой юбки при ширине ткани 150 см?

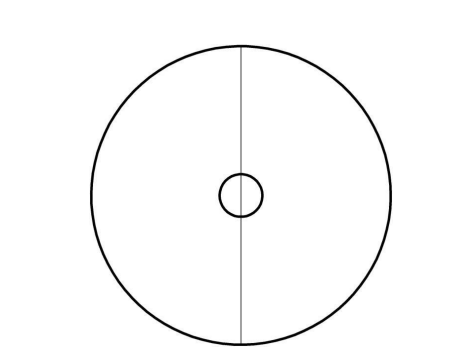
Рисунок 11 – Иллюстрация к задаче 10

11. Найдите высоту елки на городской площади имени Ленина в Кургане, если известно, что площадь основания каркаса елки равна 9 м2, а объем конуса – 45 м3 (рисунок 12).

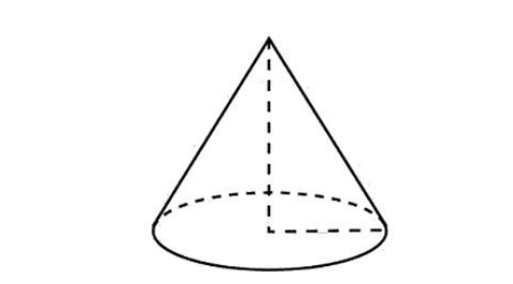
Рисунок 12 – Иллюстрация к задаче 11

12. Сколько зубцов имеет колесо зубчатой передачи (рисунок 13), если дуга окружности этого колеса, заключенная между двумя соседними зубцами, равна 12 градусов?

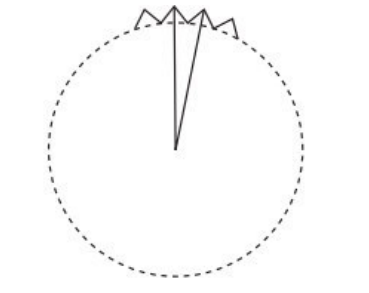
Рисунок 13 – Иллюстрация к задаче 12

13. Длина экватора земного шара примерно равна 40000 км. На сколько метров увеличился бы этот экватор, если бы радиус земного шара увеличился на 1 м? Примите π ≈3.

14. Телега проехала 5,4 км. Диаметры ее переднего и заднего колес равны соответственно 90 см и 60 см (рисунок 14). На сколько больше оборотов сделает переднее колесо по сравнению с задним? (Примите π ≈ 3).

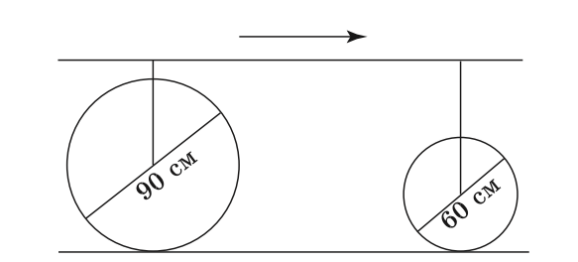
Рисунок 14 – Условие задачи 14

15. Длина минутной стрелки часов в торгово-развлекательном центре приблизительно равна 12 см. Какой путь (в миллиметрах) проходит ее конец за 1 мин? (Примите π ≈3.)

16. В городе Кургане на заседании комиссии по облагораживанию пришкольных территорий предложили позвать представителей от нескольких школ. Какое наибольшее число представителей можно пригласить, чтобы на каждого человека приходилось не менее 60 см длины дуги окружности стола, радиус которого равен 1 м, учитывая, что помимо школьных представителей в заседании участвуют глава города и представитель из Курганской городской Думы.

17. Диаметр озера Крутали равен 5 метров. Внутри озера находится островок, диаметр которого равен 1,4 метра (рисунок 15). Найдите площадь озера. Примите π ≈ 3.

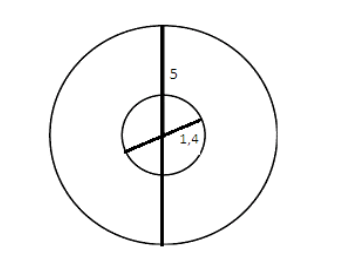
Рисунок 15 – Иллюстрация к задаче 17

18. Телеграфный столб высотой 8 м виден под углом 30 градусов. Найдите расстояние до него. В ответе укажите целое число метров. (Примите π ≈ 3).

19. Минимальная глубина заложения канализации зависит от диаметра трубопровода и вычисляется по таблице 2.

Таблица 2 – Нормы глубины заложения канализации

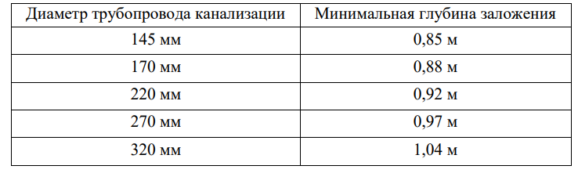
Известно, что площадь внутреннего сечения трубы составляет 1256 см2, а толщина стенок равна 2 см. На какую минимальную глубину, согласно таблице, необходимо заложить канализацию? Примите π ≈ 3,14.

20. Поле стадиона «Центральный» имеет форму прямоугольника с примыкающими к нему с двух сторон полукругами (рисунок 16). Длина беговой дорожки вокруг поля равна 400 м. Длина каждого из двух прямолинейных участков дорожки равна 100 м. Найдите ширину l поля стадиона.

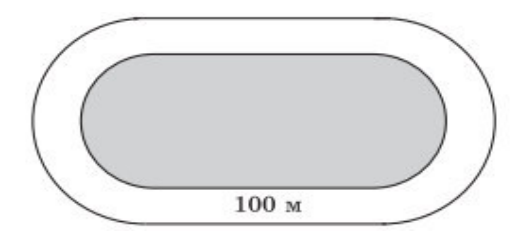
Рисунок 16 – Иллюстрация к задаче 20

21. У кондитера заказали торт в форме винтовой лестницы, для этого он решил от каждого коржа отрезать кусочек равный 1/16 окружности, лестница получится благодаря повороту коржа (рисунок 17).

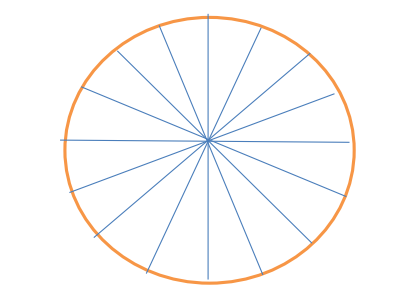
Рисунок 17 – Иллюстрация к задаче 21

Требованием покупателя было 1,5 оборота лестницы. Сколько кондитеру необходимо выпечь коржей?